Windberechnung – wie funktioniert das überhaupt?
Die Geschichte der Entstehung von anemoi ist relativ lang. Schon Jahre bevor ich mit dem Projekt an die Öffentlichkeit gegangen bin, habe ich mit einzelnen Segelfliegern immer wieder Gespräche über das Interesse an einem schnellen, genauen Standalone-Windanzeigegerät geführt. Daraus habe ich vor allem zwei Dinge mitgenommen: 1) Die Nachfrage nach einem solchen Gerät ist offensichtlich sehr groß, und 2) Es bestehen viele Missverständnisse über das Thema der Windbestimmung. Die Vorstellungen reichen von “Das ist doch ganz einfach, man muss ja nur das Winddreieck auflösen” bis hin zur Meinung, es sei überhaupt nicht möglich, den Wind insbesondere im Geradeausflug hinreichend genau zu bestimmen. Beides stimmt nicht – die Wahrheit ist bedeutend komplexer. In diesem Artikel möchte ich versuchen, die technischen Grundlagen verständlich zu vermitteln.
Natürlich basiert jeder Ansatz zur Windbestimmung auf dem Winddreieck, das jeder Flugschüler bereits im Navigationsunterricht zeichnen musste (und danach wahrscheinlich nie wieder verwendet hat). Klar: theoretisch genügt es, Länge und Richtung des Ground-Vektors und des Airspeed-Vektors zu kennen, um deren Differenz – den Windvektor – zu ermitteln. Für den Ground-Vektor stehen normalerweise hinreichend genaue GPS-Informationen zur Verfügung. Die Länge des Airspeed-Vektors bekommt man vom Fahrtmesser (Ha! Erster Denkfehler! Es ist nicht die angezeigte Fahrt, sondern die True Airspeed, welche sich aus dem Staudruck und der Luftdichte berechnet und sich von der Fahrtmesseranzeige ganz drastisch unterscheiden kann). Die Ausrichtung des Airspeed-Vektors bekommt man vom Magnetkompass, nicht wahr? Insgesamt stehen den zwei Unbekannten (der Windrichtung und Windstärke) auch zwei Gleichungen gegenüber, die sich ergeben wenn man jeweils die Nord- und Ostkomponenten des Ground- und Airspeedvektors voneinander abzieht. Mathematisch funktioniert das also perfekt.
Stellen wir uns nun einmal ein Beispiel vor, in dem ein Segelflugzeug mit 130 km/h True Airspeed unterwegs ist, und dabei einem Seitenwind von 20 km/h ausgesetzt ist. Im oberen Teil der gleich folgenden Graphik ist für dieses Beispiel das Winddreieck dargestellt. Aber vorher stellen wir uns der Realität: auch wenn wir ein gutes GPS, also den Ground-Vektor, und eine mit Druck und Temperatur genau kalibrierte True Airspeed, also die Länge des Airspeed-Vektors haben: Mit dem Heading, also der Richtung des Airspeed-Vektors, könnte es ein Problem geben. Ist der Magnetkompass korrekt kalibriert? Stimmt die Deviationstabelle? Wie groß ist die Ortsmissweisung? Ist der Faden schief, so dass zusätzlich ein Schiebewinkel im Spiel ist? Ich habe in einem einzigen Atemzug gerade mindestens vier Gründe aus dem Ärmel geschüttelt, die dazu beitragen, dass es fast nicht möglich ist, die Richtung des Airspeed-Vektors aufs Grad genau zu kennen. In Wirklichkeit gibt es noch mehr davon. Nehmen wir also einmal wohlwollend an, dass das Heading, wenn schon nicht ganz genau, dann zumindest mit einem optimistisch kleinen Fehler von nur drei Grad bekannt ist. Und nun bilden wir das Winddreieck und ermitteln den Wind. Dies zeigt der untere Teil der Graphik.

Siehe da: Anstatt der wahren 20 km/h führen die drei Grad Heading-Fehler zu einem Ergebnis von 28 km/h Windstärke. Dies ist ein stattlicher Fehler von 40 Prozent, und man muss sich daran erinnern, dass wir sehr optimistisch waren. Was, wenn das Segelflugzeug nicht 130, sondern 200 km/h fliegt, und der Heading-Fehler eher 5 Grad beträgt? (Antwort: 85 Prozent Fehler).
Was ist die Moral? Nun, wer den Wind ordentlich berechnen möchte, der hat zwei Möglichkeiten. Entweder man sorgt sich neben der (durchaus machbaren) genauen Kenntnis von Groundvektor und True Airspeed insbesondere um eine absolut exakte Kenntnis des Heading (wie auch immer man das machen möchte), oder man überlegt sich eben einen anderen Ansatz.
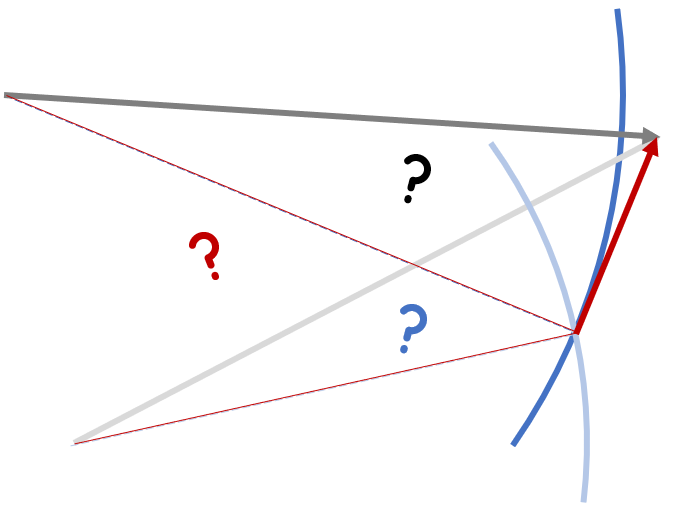
Was ist besser als ein Winddreieck? Antwort: Zwei Winddreiecke! In der nächsten Graphik ist als oberes Dreieck das allererste Beispiel noch einmal dargestellt – diesmal allerdings ist der Airspeedvektor gestrichelt, damit klar ist, dass wir seine Richtung (das Heading) überhaupt nicht kennen, sondern nur seine Länge (die True Airspeed). Ohne Heading könnte der Windvektor nun fast beliebig liegen, solange er an der Spitze des Groundvektors endet und im korrekten Abstand (der True Airspeed) vom Fuß des Groundvektors beginnt – also auf einem Kreisbogen. Nun denken wir uns ein zweites solches Winddreieck hinzu, nachdem das Flugzeug seine Flugrichtung geändert hat. Wieder ist das Heading unbekannt, aber wieder kann der Windvektor dank der bekannten Airspeed nur auf einem Kreisbogen um den Fuß des neuen Groundvektors liegen. Nun passiert etwas interessantes: Die beiden Kreisbögen schneiden sich an genau einem Punkt! Es gibt also nur noch einen einzigen möglichen Windvektor, der in die Kinematik dieser Situation passt.

Wenn wir annehmen, dass sich in dem kurzen Zeitraum der Windvektor nicht geändert hat, haben wir soeben den Wind ermittelt, ohne das Heading überhaupt kennen zu müssen. Und es kommt noch besser: Auch wenn es jetzt gar nicht mehr gebraucht wird, lässt sich das Heading von beiden Zeitpunkten (vor und nach der Kurve) nun sogar auch noch ermitteln. Es lohnt sich also, nicht nur einen “Schnappschuss” zu betrachten, sondern stattdessen die Entwicklung des Winddreiecks über die Zeit zu beobachten.
(Für die Mathe-Affinen Leser: Die beiden Winddreiecke liefern insgesamt vier Gleichungen, so dass wir auch vier Unbekannte ermitteln können: Zwei davon können neben den beiden Windkomponenten frei gewählt werden. Allerdings bietet es sich natürlich an, genau die zwei zu nehmen, über die man am wenigsten weiß. Und in den allermeisten Fällen sind dies eben die Werte für das Heading vor und nach der Kurve.)
Es ist offensichtlich, dass die oben genannte Strategie nicht auf die Paarung von nur zwei Winddreiecken beschränkt ist. Werden drei oder noch viel mehr Zeitpunkte eingeschlossen, wird das System “überbestimmt”, so dass mehr Gleichungen als Unbekannte existieren. In diesem Fall lässt es sich nicht mehr durch analytische Rechnung lösen, weil die verschiedenen Winddreiecke sich unter Umständen leicht widersprechen und dann kein einheitlicher Schnittpunkt zwischen den oben erklärten Kreisbögen mehr entsteht, sondern eher eine “Wolke” aus mehr oder weniger nah beieinander liegenden einzelnen Schnittpunkten. Der Grund ist, dass kleine Messfehler auch im Groundvektor und der True Airspeed natürlich unvermeidbar sind, und dass sich der Wind natürlich über die Zeit ändert.
Mithilfe einer solchen “Wolke” aus Einzellösungen können wir uns aber erlauben, außer dem Heading noch weitere Systemgrößen nicht genau zu kennen. Beispielsweise lässt sich nun auch noch ein Erwartungswert für die True Airspeed, deren Messung ja eher unproblematisch ist, nachträglich für alle Winddreiecke “rückwärts” über den ermittelten Wind bestimmen. Vergleicht man diese erwarteten Airspeed-Werte nun mit den jeweils gemessenen Werten aus dem Pitot-Rohr, so lässt sich ein mittlerer Kalibrierfaktor für die Staudruckmessung bestimmen. Dieser Faktor kann dann schon auf die nächsten Messungen angewendet werden, um bessere, also kleinere “Lösungswolken” zu erhalten. Nun haben wir also ein System geschaffen, das fähig ist, seine eigenen Messungen durch Beobachtung der Entwicklung über die Zeit selbst zu verbessern. Das ist schnell eskaliert, oder?
Eine geschlossener Algorithmus auf dieser Grundlage lässt sich als Erweiterter Kalmanfilter (EKF) formulieren. Eine interessante Herleitung, Implementierung und Analyse dieses Konzeptes wurde von Cho et al. (2011) dargelegt. Später fand es seinen Weg in die Segelflugwelt: Die Windbestimmung im Navigationsprogramm XCSoar funktioniert auf diese Weise!
Ist das Problem der Windbestimmung an diesem Punkt also schon gelöst? Nicht ganz. Zwar haben wir das “Heading” als wichtige, aber zumeist schlecht bekannte Eingangsgröße eliminiert, aber dafür haben wir uns ein weiteres Problem eingefangen, das wir mit dem ursprünglichen Winddreieck nicht hatten: Wir müssen zur Windbestimmung die Flugrichtung ändern um verschiedene Winddreiecke zu generieren, und der Wind zwischen zwei solchen Zeitpunkten muss weitgehend konstant sein.
Bisher haben wir als Informationsquellen für die Windberechung nur die True Airspeed, die GPS-Informationen und den Magnetkompass (den wir aber gar nicht verwenden wollen) berücksichtigt. Die XCSoar-Implementierung ist nach aktuellem Stand der Technik das beste, was allein aus diesen beiden Mess-Quellen herauszuholen ist – und es funktioniert auch gar nicht so schlecht, solange eben keine langen Geradeausflüge ohne Richtungsänderung und Kurswechsel im Spiel sind. Doch was, wenn wir noch mehr Sensoren in die Waagschale werfen, um dieses Problem auch noch zu lösen?
Wer die obige Graphik betrachtet, erkennt natürlich, dass die verwendeten Winddreiecke nicht aufeinander liegen dürfen, weil die Kreisbögen sich dann nicht schneiden, sondern ebenfalls aufeinander liegen würden. Das Flugzeug muss also in irgendeiner Form manövrieren, damit die Windinformation verfügbar bleibt. Eine mathematisch tiefgreifendere Studie über die "Beobachtbarkeit" von Wind- und Heading-Informationen ohne Magnetsensor in Bezug auf die Art der Flugzeugbewegung wurde von Myschik (2011) durchgeführt, der analog zum oben dargestellten Prinzip zu dem Ergebnis kommt, dass Heading und Wind nur dann nicht vollständig beobachtbar sind, wenn das Flugzeug über lange Perioden unbewegt und stationär geradeaus fliegt. In neuerer Zeit analysierten Huang, Meyr et al. (2020) mit Methoden der zeitdiskreten Mathematik die Beobachtbarkeit und das dynamische Verhalten des EKF. Sie konnten zeigen, dass die zufälligen Änderungen der dreidimensionalen Luftmassenbewegung ausreichen, um mit geeigneter Sensorfusion die dreidimensionale Luftmassenbewegung in Echtzeit zu schätzen. (Prof. Heinrich Meyr ist übrigens Segelflieger bei der SFG Werdenfels)
Im letzten Jahrzehnt sind Beschleunigungsmesser und Drehratensensoren in winziger Bauform mit erstaunlicher Präzision verfügbar geworden. Ein Algorithmus zu deren Verschmelzung mit GPS- und Staudrucksensoren in einem Erweiterten Kalmanfilter (EKF) für eine Ermittlung von Position, Geschwindigkeit und Lage sowie von Sensorfehlern und Windkomponenten für kleine Flugzeugdrohnen wurde z.B. von Beard und McLain (2011) vorgestellt. Ein weiteres, davon unterschiedliches Konzept zur Datenfusion für die Navigation und Windberechnung wurde von Leutenegger (2014) vorgestellt. Da Leuteneggers Anwendungsfall primär solarbetriebene Dauerflug-Drohnen sein sollten, konnte dieser nicht ganz auf die Nutzung eines Magnetkompasses verzichten, um die Beobachtbarkeit von Heading und Wind auch auf sehr langen, unbewegten Geradeausflugstrecken immer garantieren zu können. (Stefan Leutenegger ist neben seiner akademischen Arbeit ein erfolgreicher Schweizer Segelflieger). Die Arbeit Leuteneggers hat ihren Weg ebenfalls in ein Segelflug-Variometer geschafft, welches erstmals eine nahezu in Echtzeit funktionierende, genaue Windanzeige bot.
In modernen Ansätzen wird auf dieses Konzept weiter aufgebaut: Huang, Meyr (2020) erweiterten den EKF sogar mit aerodynamischen Modellbedingungen, um neben den horizontalen Windkomponenten auch die dritte Dimension, also die vertikale Luftmassenbewegung in Echtzeit zu ermitteln – ein Ansatz, der neben der Windberechnung auch großes Potential für moderne Nettovariometer-Konzepte bietet. Deren System wurde auf einer kommerziellen Plattform implementiert und in den letzten 3 Jahren in vielen Flugstunden mit verschiedenen Flugzeugen und von verschiedenen Piloten getestet. Ein ausführlicher Artikel von Prof. Heinrich Meyr, der das Problem der dreidimensionalen Luftmassenschätzung in voller mathematischer Tiefe untersucht hat, wird voraussichtlich in der nächsten Ausgabe des "segelfliegen"-Magazins erscheinen.
Den Erweiterten Kalmanfilter, der das Herzstück von anemoi bildet, habe ich etwa parallel und unabhängig zu den neueren, oben verlinkten wissenschaftlichen Arbeiten von Huang und Meyr entwickelt. Aus persönlichem Interesse haben wir uns dennoch nachträglich ausgetauscht, um die Ergebnisse zu vergleichen. Im Vergleich zur veröffentlichten Literatur verfolgt anemoi ein etwas anderes Grundkonzept, da es nicht in Verbindung zu einem Variometer steht und damit die Notwendigkeit von aerodynamischen Modellbedingungen (Polare, etc.) zur 3D-Luftmassenschätzung wegfällt. Auch die Wahl der Modell- und Messgleichungen ist deutlich unterschiedlich, wobei natürlich der gleiche Grundgedanke dahinter steckt, der schon von Beard und McLain und später vertieft von Leutenegger verfolgt wurde. Wie genau es funktioniert? Ich versuche es mal so kurz wie möglich zu erklären:

Ein Kalmanfilter ist im Grunde ein System, das mittels Differentialgleichungen und externen Informationen einen realen Prozess in Echtzeit mit simuliert (in diesem Fall werden die Trägheitssensoren in einem kinematischen Modell verwendet, um die Bewegung und Drehung des Flugzeugs live abzubilden). Die Simulationsergebnisse werden zu diskreten Zeitpunkten (nämlich immer dann wenn neue Messungen verfügbar sind) mithilfe eines Messungs-Modells mit der Realität abgeglichen, und aus dem ermittelten Fehler werden dann Korrekturen in das Prozessmodell zurück geführt. Als Messungs-Modell dient in diesem Fall das Winddreieck. Da sowohl der Ground-Vektor als auch die True Airspeed nicht nur vom Simulationsmodell vorhergesagt wurden, sondern nun auch aus Messungen verfügbar sind, und zusätzlich stets eine simulierte Heading-Information aus dem Simulationsmodell verfügbar ist, kann über den ermittelten Fehler dieser beiden Vektoren stets eine genaue Korrektur des dritten Vektors – des Windvektors – vorgenommen werden. Der korrigierte Windvektor wird dann wieder im Prozessmodell verwendet, um die Vorhersage für die nächste „Runde“ vorzubereiten, in der die nächste Korrektur folgt. Das Prozessmodell wird dabei von anemoi 50 mal pro Sekunde, das Messungs-Modell im Schnitt etwa einmal pro Sekunde neu berechnet.
Simulationsergebnisse über viele hundert Stunden Flugzeit mit realistisch verfälschten Sensormodellen und dem Bewegungsprofil typischer Segelflüge haben gezeigt, dass der Algorithmus von anemoi in der Lage ist, durch die Nutzung von Lage-Informationen aus der Trägheitsplattform (insbesondere dem simulierten Heading) die Notwendigkeit der oben diskutierten Richtungsänderungen trotz fehlendem Magnetkompass so stark zu reduzieren, dass im Segelflug-Alltag keine der oben besprochenen Probleme mit der Beobachtbarkeit auftreten.